mathematics of bitcoin - Eric Rykwalder

One reason bitcoin can be confusing for beginners is that the technology behind it redefines the concept of ownership. To own something in the traditional sense, be it a house or a sum of  money, means either having personal custody of the thing or granting  custody to a trusted entity such as a bank. With bitcoin the case is different. Bitcoins themselves are not  stored either centrally or locally and so no one entity is their  custodian. They exist as records on a distributed ledger called the  block chain, copies of which are shared by a volunteer network of  connected computers. To “own” a bitcoin simply means having the ability  to transfer control of it to someone else by creating a record of the  transfer in the block chain. What grants this ability? Access to an ECDSA private and public key pair. What does that mean and how does that secure bitcoin? Let’s have a look under the hood. ECDSA is short for Elliptic Curve Digital Signature Algorithm. It’s a process that uses an elliptic curve and a finite field to  “sign” data in such a way that third parties can verify the  authenticity of the signature while the signer retains the exclusive  ability to create the signature. With bitcoin, the data that is signed  is the transaction that transfers ownership. ECDSA has separate procedures for signing and verification. Each  procedure is an algorithm composed of a few arithmetic operations. The  signing algorithm makes use of the private key, and the verification  process makes use of the public key. We will show an example of this  later. But first, a crash course on elliptic curves and finite fields. 

Elliptic curves

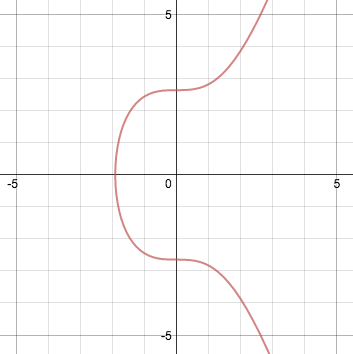
An elliptic curve is represented algebraically as an equation of the form: y2 = x3 + ax + b For a = 0 and b = 7 (the version used by bitcoin), it looks like this: 

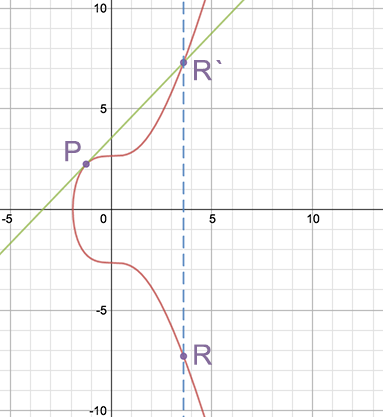
Elliptic curves have useful properties. For example, a non-vertical  line intersecting two non-tangent points on the curve will always  intersect a third point on the curve. A further property is that a  non-vertical line tangent to the curve at one point will intersect  precisely one other point on the curve. We can use these properties to define two operations: point addition and point doubling. Point addition, P + Q = R, is defined as the reflection through the x-axis of the third intersecting point R’ on a line that includes P and Q. It’s easiest to understand this using a diagram: 

Similarly, point doubling, P + P = R is defined by finding the line tangent to the point to be doubled, P, and taking reflection through the x-axis of the  intersecting point R’ on the curve to get R. Here’s an example of what that would look like: 

Together, these two operations are used for scalar multiplication, R = a P, defined by adding the point P to itself a times.  For example: R = 7P
R = P + (P + (P + (P + (P + (P + P))))) The process of scalar multiplication is normally simplified by using a  combination of point addition and point doubling operations. For  example: R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P) Here, 7P has been broken down into two point doubling steps and two point addition steps. 

Finite fields

A finite field, in the context of ECDSA, can be thought of as a  predefined range of positive numbers within which every calculation must  fall. Any number outside this range “wraps around” so as to fall within  the range. The simplest way to think about this is calculating remainders, as  represented by the modulus (mod) operator. For example, 9/7 gives 1 with  a remainder of 2: 9 mod 7 = 2 Here our finite field is modulo 7, and all mod operations over this field yield a result falling within a range from 0 to 6. 

Putting it together

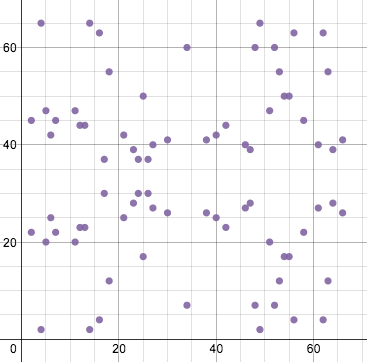
ECDSA uses elliptic curves in the context of a finite field, which  greatly changes their appearance but not their underlying equations or  special properties. The same equation plotted above, in a finite field  of modulo 67, looks like this: 

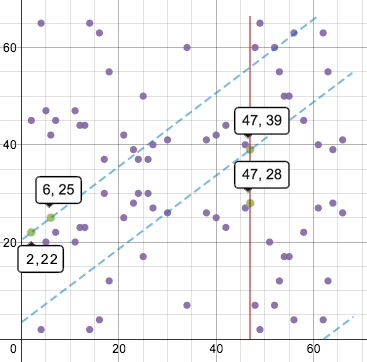
It’s now a set of points, in which all the x and y values are integers between 0 and 66. Note that the “curve” still retains its horizontal symmetry. Point addition and doubling are now slightly different visually.  Lines drawn on this graph will wrap around the horizontal and vertical  directions, just like in a game of Asteroids, maintaining the same  slope. So adding points (2, 22) and (6, 25) looks like this: 

 The third intersecting point is (47, 39) and its reflection point is (47, 28). 

Back to ECDSA and bitcoin

A protocol such as bitcoin selects a set of parameters for the  elliptic curve and its finite field representation that is fixed for all  users of the protocol. The parameters include the equation used, the prime modulo of the field, and a base point that falls on the curve. The order  of the base point, which is not independently selected but is a  function of the other parameters, can be thought of graphically as the  number of times the point can be added to itself until its slope is  infinite, or a vertical line. The base point is selected such that the  order is a large prime number. Bitcoin uses very large numbers for its base point, prime modulo, and  order. In fact, all practical applications of ECDSA use enormous  values. The security of the algorithm relies on these values being  large, and therefore impractical to brute force or reverse engineer. In the case of bitcoin: Elliptic curve equation: y2 = x3 + 7 Prime modulo = 2256 – 232 – 29 – 28 – 27 – 26 – 24 - 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F Base point = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB  2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448  A6855419 9C47D08F FB10D4B8 Order = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 Who chose these numbers, and why? A great deal of research, and a fair amount of intrigue,  surrounds the selection of appropriate parameters. After all, a large,  seemingly random number could hide a backdoor method of reconstructing  the private key. In brief, this particular realization goes by the name  of secp256k1 and is part of a family of elliptic curve solutions over  finite fields proposed for use in cryptography. 

Private keys and public keys

With these formalities out of the way, we are now in a position to  understand private and public keys and how they are related. Here it is  in a nutshell: In ECDSA, the private key is an unpredictably chosen  number between 1 and the order. The public key is derived from the  private key by scalar multiplication of the base point a number of times  equal to the value of the private key. Expressed as an equation: public key = private key * base point This shows that the maximum possible number of private keys (and thus bitcoin addresses) is equal to the order. In a continuous field we could plot the tangent line and pinpoint the public key on the graph, but there are some equations that accomplish the same thing in the context of finite fields. Point addition of p + q to find r is defined component-wise as follows: c = (qy - py) / (qx - px)
rx = c2 - px - qx
ry = c (px - rx) - py And point doubling of p to find r is as follows: c = (3px2 + a) / 2py
rx = c2 - 2px
ry = c (px - rx) - py In practice, computation of the public key is broken down into a  number of point doubling and point addition operations starting from the  base point. Let’s run a back of the envelope example using small numbers, to get  an intuition about how the keys are constructed and used in signing and  verifying. The parameters we will use are: Equation: y2 = x3 + 7  (which is to say, a = 0 and b = 7)
Prime Modulo: 67
Base Point: (2, 22)
Order: 79
Private key:  2 First, let’s find the public key. Since we have selected the simplest  possible private key with value = 2, it will require only a single  point doubling operation from the base point. The calculation looks like  this: c = (3 * 22 + 0) / (2 * 22) mod 67
c = (3 * 4) / (44) mod 67
c = 12 / 44 mod 67 Here we have to pause for a bit of sleight-of-hand: how do we perform  division in the context of a finite field, where the result must always  be an integer? We have to multiply by the inverse, which space does not  permit us to define here (we refer you to here and here if interested). In the case at hand, you will have to trust us for the moment that: 44-1 = 32 Moving right along: c = 12 * 32 mod 67
c = 384 mod 67
c = 49 rx = (492 - 2 * 2) mod 67
rx = (2401 - 4) mod 67
rx = 2397 mod 67
rx = 52 ry = (49 * (2 - 52) - 22) mod 67
ry = (49 * (-50) - 22) mod 67
ry = (-2450 - 22) mod 67
ry = -2472 mod 67
ry = 7 Our public key thus corresponds to the point (52, 7). All that work for a private key of 2! This operation - going from private to public key -  is computationally easy in comparison to trying to work backwards  to deduce the private key from the public key, which while  theoretically possible is computationally infeasible due to the large  parameters used in actual elliptic cryptography. Therefore, going from the private key to the public key is by design a one-way trip. As with the private key, the public key is normally represented by a  hexadecimal string. But wait, how do we get from a point on a plane,  described by two numbers, to a single number? In an uncompressed public  key the two 256-bit numbers representing the x and y coordinates  are just stuck together in one long string. We can also take advantage  of the symmetry of the elliptic curve to produce a compressed public  key, by keeping just the x value and noting which half of the curve the point is on. From this partial information we can recover both coordinates. 

Signing data with the private key

Now that we have a private and public key pair, let’s sign some data! The data can be of any length. The usual first step is to hash the  data to generate a number containing the same number of bits (256) as  the order of the curve. Here, for the sake of simplicity, we’ll skip the  hashing step and just sign the raw data z. We’ll call G the base point, n the order, and dthe private key. The recipe for signing is as follows:  

1. Choose some integer k between 1 and n - 1.
2. Calculate the point (x, y) = k * G, using scalar multiplication.
3. Find r = x mod n. If r = 0, return to step 1.
4. Find s = (z + r * d) / k mod n. If s = 0, return to step 1.
5. The signature is the pair (r, s)

As a reminder, in step 4, if the numbers result in a fraction (which  in real life they almost always will), the numerator should be  multiplied by the inverse of the denominator. In step 1, it is important  that k not be repeated in different signatures and that it not be guessable by a third party. That is, k  should either be random or generated by deterministic means that are  kept secret from third parties. Otherwise it would be possible to  extract the private key from step 4, since s, z, r, k and n are all known. You can read about a past exploit of this type here. Let’s pick our data to be the number 17, and follow the recipe. Our variables: z = 17 (data)
n = 79 (order)
G = (2, 22) (base point)
d = 2 (private key)  

1. Pick a random number:

k = rand(1, n - 1)
k = rand(1, 79 - 1)
k = 3  (is this really random?  OK you got us, but it will make our example simpler!)  

1. Calculate the point. This is done in the same manner as determining  the public key, but for brevity let’s omit the arithmetic for point  addition and point doubling.

(x, y) = 3G
(x, y) = G + 2G
(x, y) = (2, 22) + (52, 7)
(x, y) = (62, 63)
x = 62
y = 63  

1. Find r:

r = x mod n
r = 62 mod 79
r = 62  

1. Find s:

s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141 / 3 mod 79
s = 47 mod 79
s = 47 Note that above we were able to divide by 3 since the result was an integer. In real-life cases we would use the inverse of k (like before, we have hidden some gory details by computing it elsewhere): s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141 / 3 mod 79
s = 141 * 3-1 mod 79
s = 141 * 53 mod 79
s = 7473 mod 79
s = 47  

1. Our signature is the pair (r, s) = (62, 47).

As with the private and public keys, this signature is normally represented by a hexadecimal string. 

Verifying the signature with the public key

We now have some data and a signature for that data. A third party  who has our public key can receive our data and signature, and verify  that we are the senders. Let’s see how this works. With Q being the public key and the other variables defined as before, the steps for verifying a signature are as follows:  

1. Verify that r and s are between 1 and n - 1.
2. Calculate w = s-1 mod n
3. Calculate u = z * w mod n
4. Calculate v = r * w mod n
5. Calculate the point (x, y) = uG + vQ
6. Verify that r = x mod n. The signature is invalid if it is not.

Why do these steps work? We are skipping the proof, but you can read the details here. Let’s follow the recipe and see how it works. Our variables, once again: z = 17 (data)
(r, s) = (62, 47) (signature)
n = 79 (order)
G = (2, 22) (base point)
Q = (52, 7) (public key)  

1. Verify that r and s are between 1 and n - 1. Check and check.

r: 1 <= 62 < 79
s: 1 <= 47 < 79  

1. Calculate w:

w = s-1 mod n
w = 47-1 mod 79
w = 37  

1. Calculate u:

u = zw mod n
u = 17 * 37 mod 79
u = 629 mod 79
u = 76  

1. Calculate v:

v = rw mod n
v = 62 * 37 mod 79
v = 2294 mod 79
v = 3  

1. Calculate the point (x, y):

(x, y) = uG + vQ Let’s break down the point doubling and addition in uG and vQ separately. uG = 76G
uG = 2(38G)
uG = 2( 2(19G) )
uG = 2( 2(G + 18G) )
uG = 2( 2(G + 2(9G) ) )
uG = 2( 2(G + 2(G + 8G) ) )
uG = 2( 2(G + 2(G + 2(4G) ) ) )
uG = 2( 2(G + 2(G + 2( 2(2G) ) ) ) ) Sit back for a moment to appreciate that by using the grouping trick  we reduce 75 successive addition operations to just six operations of  point doubling and two operations of point addition. These tricks will  come in handy when the numbers get really large. Working our way from the inside out: uG = 2( 2(G + 2(G + 2( 2( 2(2, 22) ) ) ) ) )
uG = 2( 2(G + 2(G + 2( 2(52, 7) ) ) ) )
uG = 2( 2(G + 2(G + 2(25, 17)  ) ) )
uG = 2( 2(G + 2( (2, 22) + (21, 42) ) ) )
uG = 2( 2(G + 2(13, 44) ) )
uG = 2( 2( (2, 22) + (66, 26) ) )
uG = 2( 2(38, 26) )
uG = 2(27, 40)
uG = (62, 4) And now for vQ: vQ = 3Q
vQ = Q + 2Q
vQ = Q + 2(52, 7)
vQ = (52, 7) + (25, 17)
vQ = (11, 20) Putting them together: (x, y) = uG + vQ
(x, y) = (62, 4) + (11, 20)
(x, y) = (62, 63) Clearly step 5 is the bulk of the work. For the final step,  

1. Verify that r = x mod n

r = x mod n
62 = 62 mod 79
62 = 62 Our signature is valid! 

Conclusion

For those of you who saw all the equations and skipped to the bottom, what have we just learned? We have developed some intuition about the deep mathematical  relationship that exists between public and private keys. We have seen  how even in the simplest examples the math behind signatures and  verification quickly gets complicated, and we can appreciate the  enormous complexity which must be involved when the parameters involved  are 256-bit numbers. We have seen how the clever application of the  simplest mathematical procedures can create the one-way “trap door”  functions necessary to preserve the information asymmetry which defines  ownership of a bitcoin. And we have newfound confidence in the  robustness of the system, provided that we carefully safeguard the  knowledge of our private keys. In other words, this is why it is commonly said that bitcoin is “backed by math”. If you hung in through the complicated bits, we hope it gave you the  confidence to take the next step and try out the math on your own (a modular arithmetic calculator makes  the finite field math much easier). We found that going through the  steps of signing and verifying data by hand provides a deeper  understanding of the cryptography that enables bitcoin’s unique form of  ownership. 

---

Tags : Bitcoin, Cryptocurrency, Mathematics, Blockchain

---

This Post Was Published On My Steemit Blog. 
Earned : $22.03 SBD Converted to USD @0.8643$ Rate = $19.0405 USD. 
First Time heard about Steemit ? Click Here To Know...

---